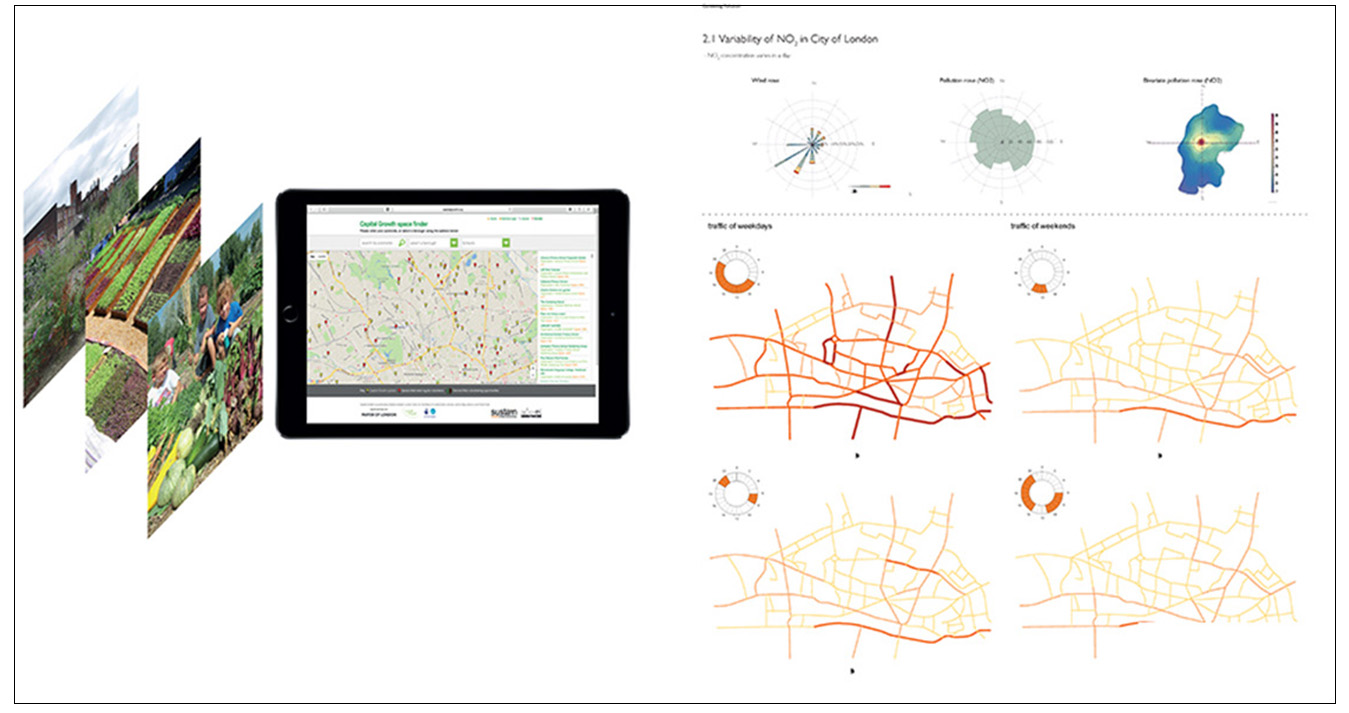
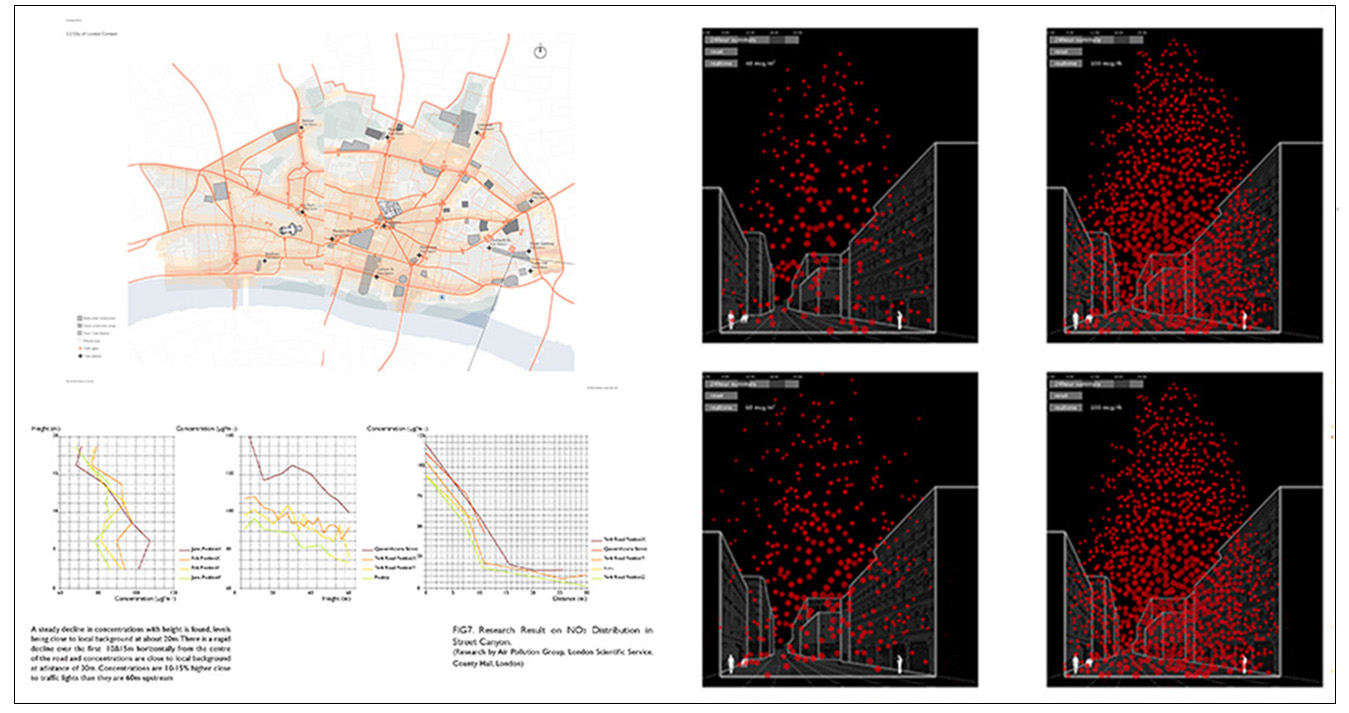
Gardening Pollution
Current urban systems rely on food and energy sources located far away from the centers of consumption. This disconnection between production and consumption results in a model with large energy and CO2 footprint, it exacerbates inequalities among urban population to access to fresh food, clean water and energy and reduces the competitive field resulting in low quality products at a higher cost. One way to tackle this problem is to decentralize the production of food and energy by allowing this production to be closer to the urban fabric at a lower scale. Lower scale production of food and energy in high dense urban environments
faces two main problems:
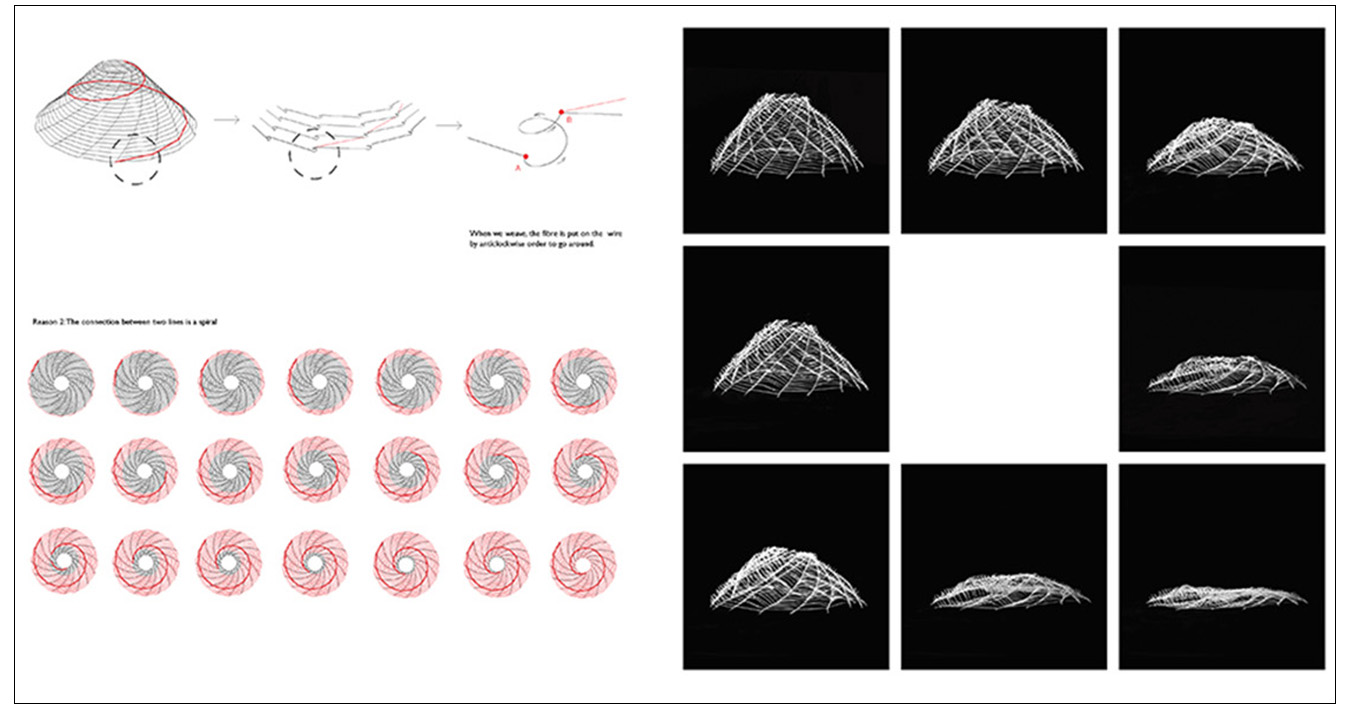
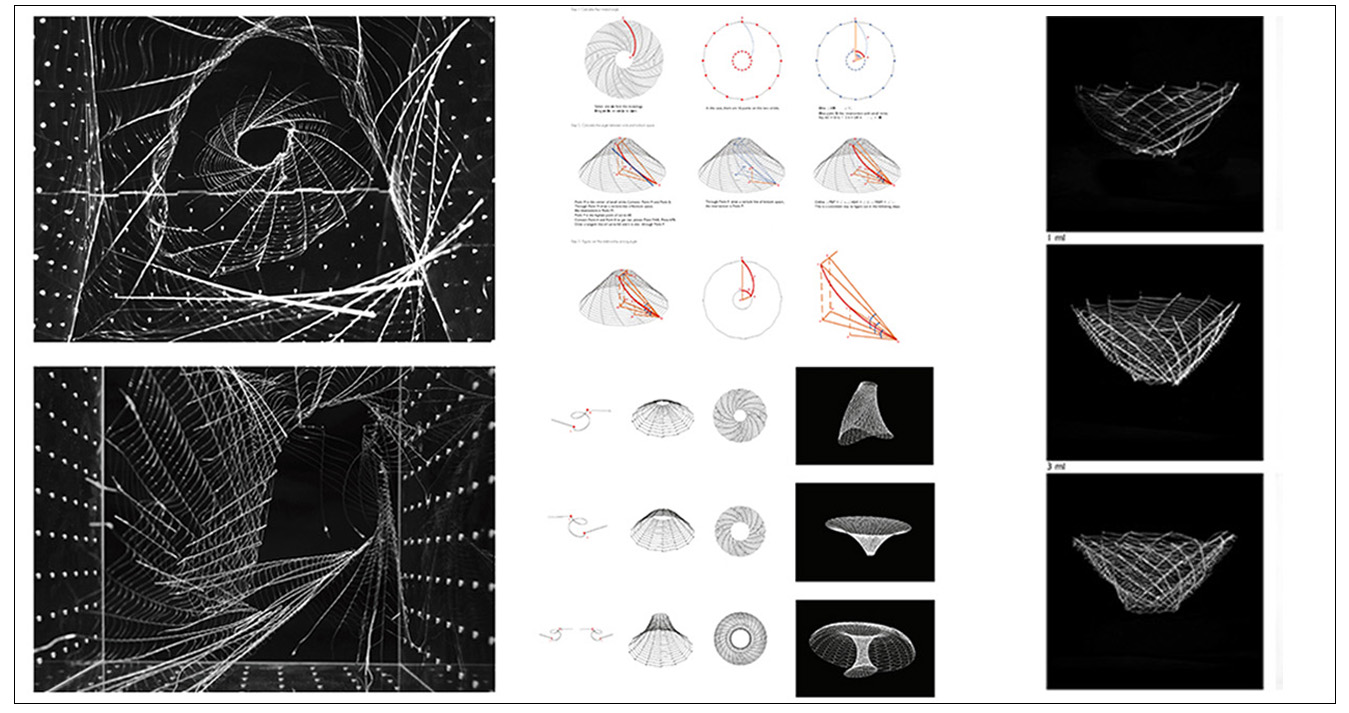
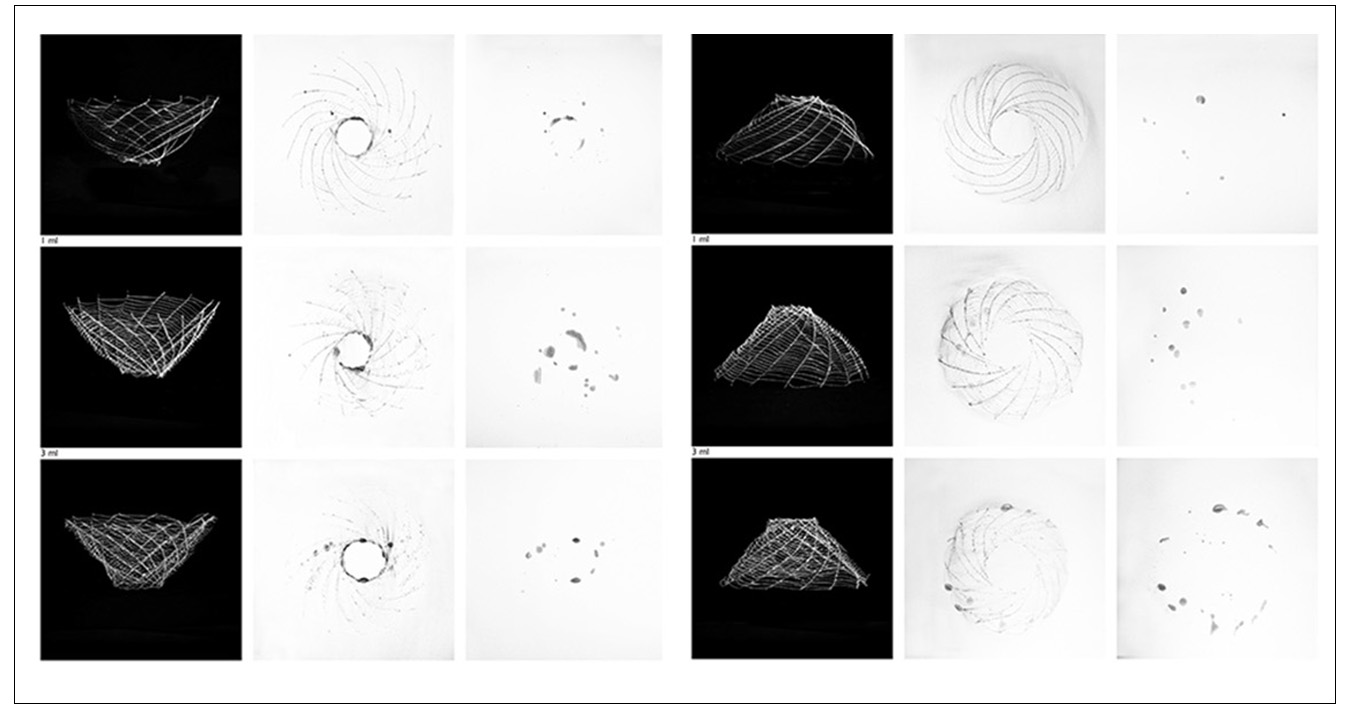
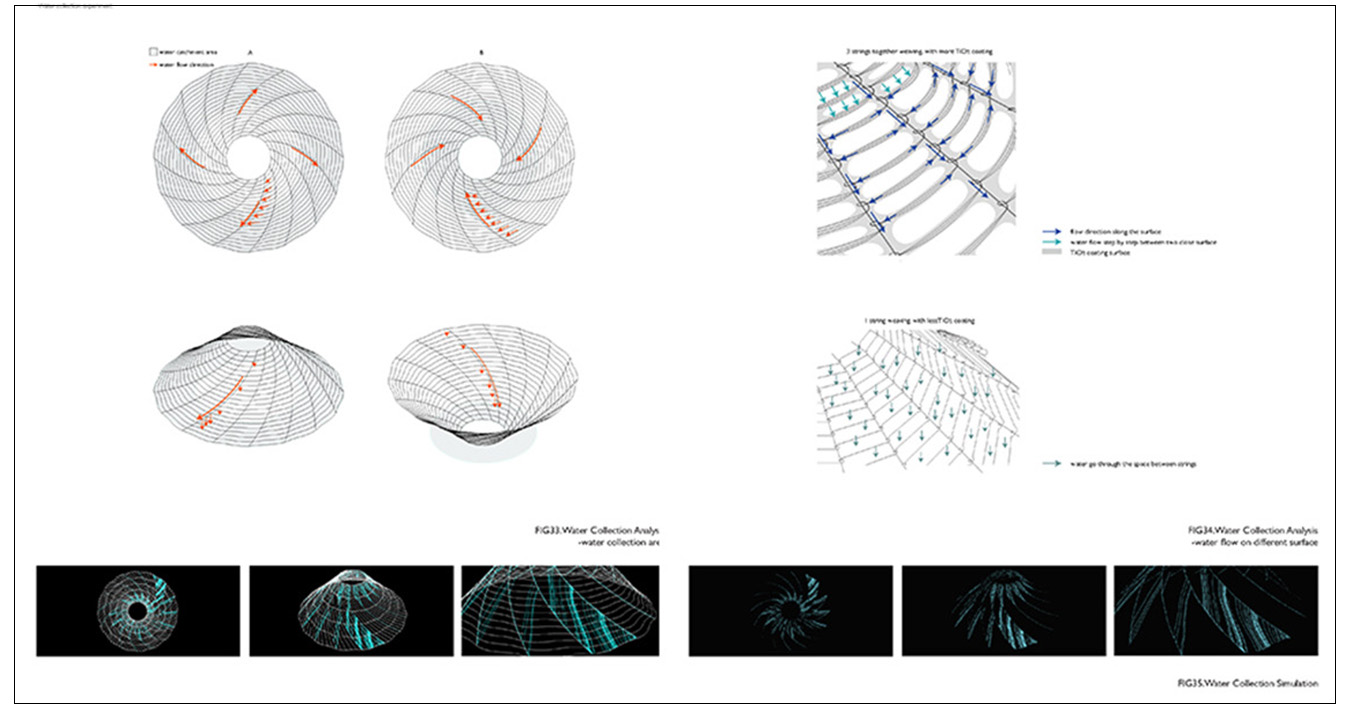
(1) How it could be implemented in the urban fabric, facilitating access to natural light and water and (2) How to compete with economies of scale. In order to address the first issue, Relational Urbanism offers a digital model that is able to optimize the location of urban built area in relation to the location of urban agricultural fields in high rise and high dense environments. It does so by taking access to natural light as a major constraint and producing an estimated timeline of how the city would grow vertically in relation to population growth. The model operates as a dynamic system constituted of different subsystems including water, agriculture and energy. These systems dynamically interact within themselves and with their environment which is considered the primary source of the energy and hydrological resources (water and sunlight).The model is employing the following software’s: Stella(Dynamic System Modelling) and Rhinoceros/Grasshopper/Python Script(A Parametric design software for architecture).It computes and measures the different variables and parameters according the local condition of light, water and climate and that in turn become the inputs for the distribution of urban massing. The model is able to generate multiple multi objective urban design solutions
- [year] 2016
- [Credits] Ana Acurio, Yan Meng, Xuezhu Zhai
- [Design Tutors] Enriqueta Llabres Valls, Zachary Flucker
- [H+T ] Nuria Alvarez
Gardening Pollution
Current urban systems rely on food and energy sources located far away from the centers of consumption. This disconnection between production and consumption results in a model with large energy and CO2 footprint, it exacerbates inequalities among urban population to access to fresh food, clean water and energy and reduces the competitive field resulting in low quality products at a higher cost. One way to tackle this problem is to decentralize the production of food and energy by allowing this production to be closer to the urban fabric at a lower scale. Lower scale production of food and energy in high dense urban environments
faces two main problems:
(1) How it could be implemented in the urban fabric, facilitating access to natural light and water and (2) How to compete with economies of scale. In order to address the first issue, Relational Urbanism offers a digital model that is able to optimize the location of urban built area in relation to the location of urban agricultural fields in high rise and high dense environments. It does so by taking access to natural light as a major constraint and producing an estimated timeline of how the city would grow vertically in relation to population growth. The model operates as a dynamic system constituted of different subsystems including water, agriculture and energy. These systems dynamically interact within themselves and with their environment which is considered the primary source of the energy and hydrological resources (water and sunlight).The model is employing the following software’s: Stella(Dynamic System Modelling) and Rhinoceros/Grasshopper/Python Script(A Parametric design software for architecture).It computes and measures the different variables and parameters according the local condition of light, water and climate and that in turn become the inputs for the distribution of urban massing. The model is able to generate multiple multi objective urban design solutions